Statistics homework 3
Theory: Explain what are marginal, joint and conditional distributions and how we can explain the Bayes theorem using relative frequencies. Explain the concept of statistical independence and why, in case of independence, the relative joint frequencies are equal to the products of the corresponding marginal frequencies.
Practice:
-
Create a program to read data from a CSV file, and store it into a suitable collection of suitably designed objects, for further processing. Compute mean and standard deviation and frequency distribution for at least one of the variable, and for one pair of variables.
-
Compute a frequency distribution of the meaningful words from any text file and create a personal graphical representation of the corresponding “word cloud” (in case, can use animation if you wish), keeping into account the frequencies of the words.
Practice theory:
-
Do a review about charts useful for statistics and data presentation (example of some: StatCharts.txt ). What is the chart type that impressed you most and why ?
-
Do a comprehensive research about the GRAPHICS object and all its members (to get ready to create any statistical chart.)
Theory 1
Marginal, joint and conditional distribution
Marginal distribution
When we work with a multivariate dataset, we can compute the distribution separately for each variable, like we had multiple univariate datasets. In this case, each distribution is called a marginal distribution.
Joint distribution
Having a bivariate dataset we can create intervals of values for both variables and put these intervals into a matrix where in each cell we have the joint frequency of values that falls into both intervals described by row and column.
Conditional distribution
Having, as above, a bivariate distribution and computing the frequencies in a matrix called contingency table, we can compute throughout this structure also the conditional distribution on the condition of the two variables. For instance if we have two variables \(X\) and \(Y\) and we put the intervals of \(X\) as rows and the intervals of \(Y\) as columns i can say that each column is a conditional distribution of \(X\) on condition of \(Y\) falling in some category and that each row is a conditional distribution of \(Y\) on condition of \(X\) falling in some category
Schema
Having a bivariate dataset, we can build a contingency table:
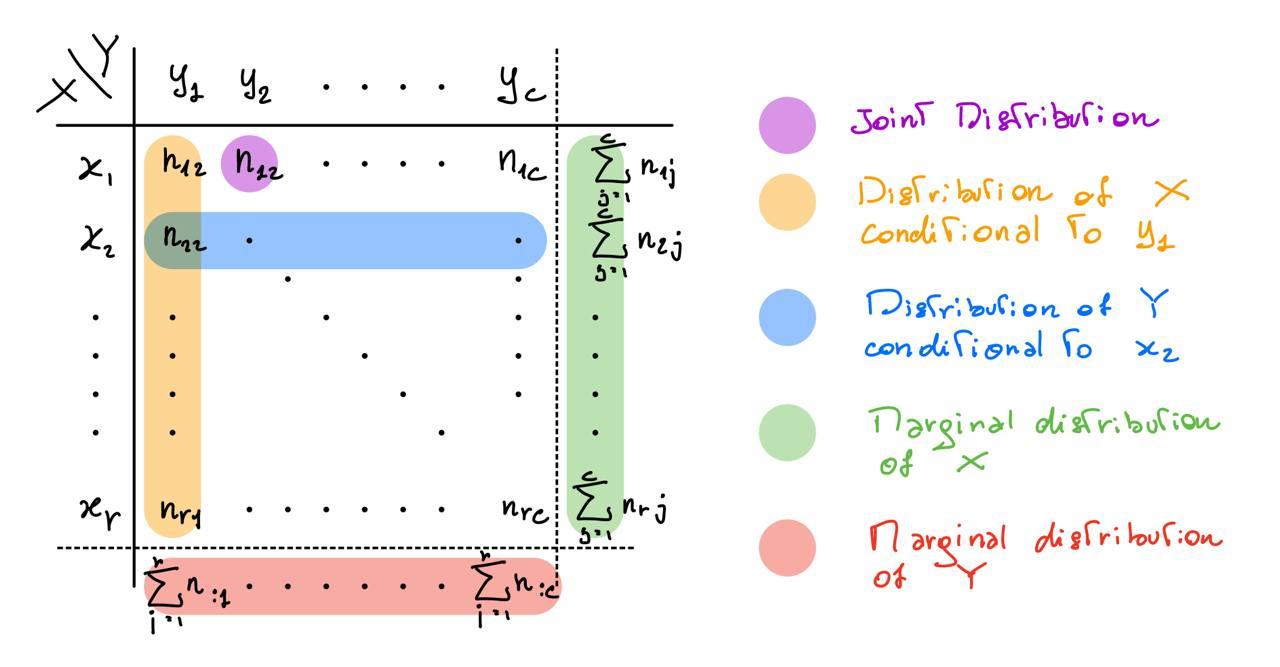
Bayes theorem using relative frequencies
The Bayes’ theorem is this:
\[P(X=x | Y=y) = \frac{P(X=x, Y=y)}{P(Y=y)}\]we can build this equation using relative requencies. Having a bivariate distribution of two variables \(X\) and \(Y\) and putting the frequencies in a contingency table as above we can write the relative frequency for a generic \(n_{ij}\) as follows:
\[\frac{n_{ij}}{\sum_{i = 1}^{r} x_{ij}} = \frac{n_{ij}}{n} \cdot \frac{n}{\sum_{i = 1}^{r} x_{ij}} = \frac{\frac{n_{ij}}{n}}{\frac{\sum_{i = 1}^{r} x_{ij}}{n}}\]where \(n\) is the total number of observations, \(\frac{n_{ij}}{\sum_{i = 1}^{r} x_{ij}}\) is the frequency of \(x_{i}\) conditional to \(y_{j}\), \(\frac{n_{ij}}{n}\) is the relative frequency of \((x_{i}, y_{j})\) and \(\frac{\sum_{i = 1}^{r} x_{ij}}{n}\) is the relative frequency of \(y_{j}\).
We can see that equation above in other terms like as follows:
\[Freq(X=x_{i} | Y=y_{j}) = \frac{Freq(X=x_{i}, Y=y_{j})}{Freq(Y=y_{j})}\]Interpreting frequencies as probabilities we have the Bayes’ theorem.
Statistical independence
We say that two variables are independent if:
\[\forall i \in \{1, \dots, r\}, \forall j, k \in \{1, \dots, c\} \land k\neq j \ \implies \ Freq(X=x_{i} | Y=y_{j}) = Freq(X=x_{i} | Y=y_{k}) = Freq(X=x_{i})\]This implies that the relative joint probability is equal to the product between the marginal frequencies:
\[Freq(X = x_{i} \land Y=y_{j}) = Freq(X = x_{i}) \cdot Freq(Y=y_{j})\]This because if \(X\) is independent from \(Y\) also \(Y\) is indipendent from \(X\) and from this we have that:
\[Freq(X=x_{i} | Y=y_{j}) = Freq(X=x_{i}) \iff Freq(Y=y_{j} | X=x_{i}) = Freq(Y=y_{j})\]This implies that:
\[Freq(X=x_{i} \land Y=y_{j}) = Freq(X=x_{i} | Y=y_{j}) \cdot Freq(Y=y_{j}) =\] \[= Freq(X=x_{i}) \cdot Freq(Y=y_{j})\]Practice 1
Since i decided to make the program indipendent from the csv file, i created a generic class for csv reading that maps rows to a list of dictionaries where the key is the column name and the value is the element in the cell for that row and column:
public class CSVData
{
public List<Dictionary<string, object>> data;
public List<string> titles;
public CSVData(string[] titles)
{
data = new List<Dictionary<string, object>>();
this.titles = new List<string>(titles);
}
public void addRow(string[] row)
{
Dictionary<string, object> newRow = new Dictionary<string, object>();
NumberFormatInfo formatProvider = new NumberFormatInfo();
formatProvider.NumberDecimalSeparator = ".";
for (int i = 0; i < row.Length; i++)
{
Console.WriteLine(row[i]);
try
{
newRow[titles[i]] = (double)Convert.ToDouble(row[i], formatProvider);
} catch {
newRow[titles[i]] = row[i];
}
}
data.Add(newRow);
}
public double computeMean(string variable)
{
double mean = 0;
int elements_number = 0;
try {
foreach (Dictionary<string, object> row in data)
{
elements_number++;
mean += ((double)row[variable] - mean)/elements_number;
Console.WriteLine((double)row[variable]);
}
} catch
{
return 0;
}
return mean;
}
public double computeSD(string variable)
{
double mean = computeMean(variable);
double sum = 0;
int elements_number = 0;
try
{
foreach (Dictionary<string, object> row in data)
{
elements_number++;
sum += Math.Pow(Math.Abs((double)row[variable] - mean), 2);
}
} catch
{
return 0;
}
return Math.Sqrt(sum / elements_number);
}
public Dictionary<object, double> computeUnivariateDistribution(string variable)
{
DiscreteDistribution<object> d = new DiscreteDistribution<object>();
foreach (Dictionary<string, object> row in data)
{
d.updateFrequency((row[variable]));
}
return d.getDistribution();
}
public Dictionary<(object, object), double> computeBivariateDistribution(string variable1, string variable2)
{
DiscreteDistribution<(object, object)> d = new DiscreteDistribution<(object, object)>();
foreach (Dictionary<string, object> row in data)
{
d.updateFrequency((row[variable1],row[variable2]));
}
return d.getDistribution();
}
}
How it works
Practice 2
The core code is the following:
public partial class Form1 : Form
{
Bitmap b;
public Form1()
{
InitializeComponent();
b = new Bitmap(pictureBox1.Width, pictureBox1.Height);
}
private void openFileToolStripMenuItem_Click(object sender, EventArgs e)
{
OpenFileDialog openFileDialog = new OpenFileDialog();
openFileDialog.ShowDialog();
string filename = openFileDialog.FileName;
worldCloud(filename);
}
private void worldCloud(string filename)
{
List<string> words = new List<string>();
using (StreamReader r = new StreamReader(filename))
{
string s = string.Empty;
int i = 0;
while ((i = r.Read()) != -1)
{
Char c = Convert.ToChar(i);
if (Char.IsDigit(c) || Char.IsLetter(c))
{
s = s + c;
}
else
{
if (s.Trim() != string.Empty)
words.Add(s);
s = string.Empty;
}
}
}
DiscreteDistribution<string> d = new DiscreteDistribution<string>();
foreach (string word in words)
{
d.updateFrequency(word);
}
Dictionary<string, double> distribution = d.getDistribution();
var sortedDistribution = from entry in distribution orderby entry.Value descending select entry;
List<Rectangle> rectList = new List<Rectangle>();
Graphics g = Graphics.FromImage(b);
foreach (KeyValuePair<string, double> kvp in sortedDistribution)
{
Rectangle rect;
Font f = new Font(new FontFamily("arial"), (float)(kvp.Value * 500));
Size s = Size.Truncate(g.MeasureString(kvp.Key, f));
Console.WriteLine((float)(kvp.Value * 10));
int tries = 0;
Random r = new Random();
do
{
tries++;
int x = r.Next(pictureBox1.Left, pictureBox1.Right - (s.Width+3));
int y = r.Next(pictureBox1.Top, pictureBox1.Bottom - (s.Height+3));
rect = new Rectangle(new Point(x, y), s);
} while (rectangleContained(rect, rectList) && tries < 1000);
g.DrawString(
kvp.Key,
f,
new SolidBrush(Color.FromArgb(r.Next(0, 256), r.Next(0, 256), r.Next(0, 256))),
new Point(rect.X, rect.Y)
);
rectList.Add(rect);
}
pictureBox1.Image = b;
}
private bool rectangleContained(Rectangle rect, List<Rectangle> rectList)
{
foreach (Rectangle r in rectList)
{
if (r.Contains(rect) || r.IntersectsWith(rect) || rect.Contains(r))
{
return true;
}
}
return false;
}
}
}
How it works
Download projects
Practice Theory 1
One fundamental step in the ending of a statistical analysis is the analyzed data visualization. This is achieved using various forms of charts that put in evidence different aspects and don’t show some others.
Personally, I don’t have a preferred chart, I think each chart is useful for certain kind of data and visualizations. I see graphs as tools, and it’s difficult to have a favorite tool if every of them is useful for something different.
I will make a list of some common chart used in statistical data visualization
Bar graph
A bar graph is a way to visually represent qualitative data. Data is displayed either horizontally or vertically and allows viewers to compare items, such as amounts, characteristics, times, and frequency.
Pie charts
This kind of graph is helpful when graphing qualitative data, where the information describes a trait or attribute and is not numerical
Histogram
Histograms are another kind of graphs that uses bars. This type of graph is used with quantitative data. Ranges of values, called classes, are listed at the bottom, and the classes with greater frequencies have taller bars.
Histograms are used with variables that cannot be quantified like opinions or feelings, differently by Bar charts that are used to quantifiable variables.
Scatter plots
A scatter plot displays data that is paired by using a horizontal axis (the x-axis), and a vertical axis (the y-axis). Usually, scatter plots are correlated to regression analysis on the data to view what function fits best on the data trend.
Practice Theory 2
As described in [1] the Graphics object represents a GDI+ drawing surface, and is the object that is used to create graphical images.
A graphics object can be created in a variety of ways.
- Receive a reference to a graphics object as part of the PaintEventArgs in the Paint event of a form or control.
- Call the CreateGraphics method of a control or form to obtain a reference to a Graphics object that represents the drawing surface of that control or form.
- Create a Graphics object from any object that inherits from Image.
To draw every shape, we need a Pen object:
System.Drawing.Pen myPen;
myPen = new System.Drawing.Pen(System.Drawing.Color.Tomato);
To fill the shape, we need a SolidBrush object:
System.Drawing.SolidBrush myBrush = new System.Drawing.SolidBrush(System.Drawing.Color.Red);
System.Drawing.Graphics formGraphics;
formGraphics = this.CreateGraphics();
formGraphics.FillEllipse(myBrush, new Rectangle(0, 0, 200, 300));
myBrush.Dispose();
formGraphics.Dispose();
The Graphics object has some method to draw shapes as:
- DrawLine
- DrawEllipse
- DrawRectangle
- DrawArc
- DrawPie
- DrawPolygon
- DrawBezier
- DrawString